AtomicDensityMatrix`
AtomicDensityMatrix`
Component
Component[tens,q]
extracts the q‐th component of a spherical tensor tens.
Component[cart,i]
extracts the i‐th component of a Cartesian vector cart.
Component[decomp, k]
extracts the spherical tensor of rank k from a tensor decomposition decomp.
Component[op,{m1,m2}]
extracts the matrix element corresponding to sublevels with angular‐momentum‐projection quantum numbers m1 and m2 from an operator op.
Component[sys,op,{s1,s2}]
extracts the matrix element of operator op corresponding to the states s1 and s2 of atomic system sys.
Component[sys,mat,{s1,s2}]
extracts the tensor decomposition from the tensor‐decomposition matrix mat corresponding to the states s1 and s2.
Details and Options
- The component index q must be a integer or half-integer from the range
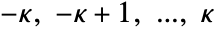, where 
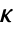is the rank of the spherical tensor. - The quantum numbers mi be a integers or half-integers from the range
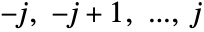, where 
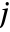is the rank of the operator. - The Cartesian component index i must be a positive integer.
- Additional indices or states ni may be given as Component[tens,n1,n2,…] or Component[sys,tens,n1,n2,…] to extract a component from a nested tensor structure. The index n1 refers to the top-level tensor, the index n2 to the second level, and so on.
- Component[tens] extracts the single component from a rank‐zero tensor, the single matrix element from a rank-zero operator, or the single tensor decomposition from a tensor‐decomposition matrix for a single angular-momentum state.
