AtomicDensityMatrix`
AtomicDensityMatrix`

WignerEckart

WignerEckart[sys, {op, k}]

returns the covariant tensor representing the rank‐k operator op with respect to the basis states of the atomic system sys.

WignerEckart[sys, {op,k,q}]

returns the q‐th component of the tensor operator.

WignerEckart[state1,{op,k,q},state2]

returns the matrix element of the operator between the atomic states state1 and state2.

WignerEckart[j,{op,k}]

returns the operator for a Zeeman system with angular momentum equal to integer or half-integer j.

Details and Options

  • WignerEckart finds the matrix elements of an operator 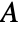in terms of the reduced matrix element of 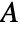using the Wigner—Eckart theorem:
  •     
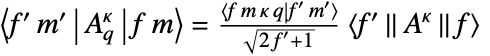
  • Reduced matrix elements for some operators are defined in the ADM package. If an unknown operator is supplied, the matrix elements will be written in terms of placeholder values for the reduced matrix elements.
  • Operators with defined reduced matrix elements include Energy, Polarization, J, L, S, Dipole, MagneticMoment, Polarizability, GroundState and ExcitedState.
  • WignerEckart takes the following options:
  • Representation Automaticthe basis to represent the tensor operator
    AllowedCouplings Allmatrix elements that are allowed to be nonzero
  • Representation takes the values "Zeeman", "PolarizationMoments", or Automatic, where Automatic means that the default option value set for DensityMatrix is used.

Examples

open allclose all

Basic Examples  (3)

Define a system:

Matrix elements of the Energy operator for the system:

The three covariant components of the J operator in the spherical basis:

If an unknown operator is supplied, the result is in terms of the symbolic reduced matrix elements:

A single matrix element:

The J operator for a generic Zeeman system with :

Scope  (4)

Types of atomic systems  (3)

An operator for a toy (no angular momentum) system:

An operator for a Zeeman system:

An operator for a hyperfine-Zeeman system:

RowBox[{"Operators", " ", "of", " ", "different", " ", "rank"}]  (1)

Define a system:

The rank-zero GroundState operator (returns 1 for states with zero natural width), with one component:

The rank-one L operator, with three components:

The rank-two (tensor) Polarizability operator, with five components:

Options  (2)

AllowedCouplings  (1)

By default, the dipole operator can connect any pair of states of opposite parity:

We can artificially set certain matrix elements to zero by restricting the AllowedCouplings:

Representation  (1)

The J operator in the Zeeman basis:

Return the operator in terms of the basis of polarization moments:

Properties & Relations  (1)

To obtain the Cartesian components of a vector operator, use ToCartesian. The , , and components of the spin-1/2 J operator:

These are equal to 1/2 the Pauli matrices: