Decomposition
Decomposition[op]
returns the expansion coefficients of the decomposition of a rank‐
operator op (e.g., the density matrix) as a sum of polarization moments.
Decomposition[sys, op]
returns a matrix of expansion coefficients for the decomposition of an operator on an atomic system sys.
Details and Options
- Decomposition returns either a single tensor decomposition object or a matrix of such objects, each consisting of a list of (contravariant) spherical tensors of increasing rank.
- The decomposition of a rank-
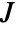operator [i.e., a 
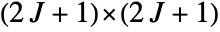matrix] is a list of 
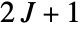spherical tensors of rank zero through 
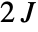. - Decomposition can also decompose a spherical tensor or Cartesian vector operator, returning a vector or tensor of decompositions.
- The original operator can be recovered using Recomposition.
- TensorForm can be used to display a tensor decomposition as a list of row or column vectors.
Examples
open allclose allBasic Examples (2)
The tensor decomposition of a 
operator:
Display the decomposition as a list of column vectors using TensorForm:
Check that it has the form of a contravariant tensor decomposition:
An atomic system consisting of a 
state and a 
state:
Find the matrix of tensor decompositions for the density matrices of the two states and the coherences between the states:
Check that it has the form of a matrix of tensor decompositions:
Properties & Relations (3)
The tensor-decomposition components are given by the trace of the product of the operator with the polarization operators.
operator:The set of polarization operators for a 
space:
The trace of operator times polarization operators:
This is equal to the decomposition of the operator:
The operator can be recovered using Recomposition:
A tensor decomposition can be supplied to AMPSPlot: