AtomicDensityMatrix`
AtomicDensityMatrix`
EffectiveHamiltonian
EffectiveHamiltonian[h,u,t]
returns the effective Hamiltonian corresponding to the Hamiltonian h under a (possibly time dependent) transformation u, assuming time variable t.
Details and Options
- EffectiveHamiltonian finds the operator that satisfies the Schrödinger equation in the frame determined by the transformation matrix, even if that frame is non-inertial.
- The formula for the effective Hamiltonian is
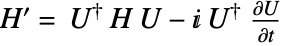 .
. - EffectiveHamiltonian is called by RotatingWaveApproximation.
Examples
Basic Examples (1)
Define a system with Zeeman structure:
Find the Hamiltonian assuming a single optical field of frequency ω:
Find a unitary transformation for performing the rotating-wave approximation using RotatingWaveTransformMatrix:
This matrix can be supplied to the function EffectiveHamiltonian to transform the Hamiltonian to the rotating frame without dropping the fast-oscillating terms: