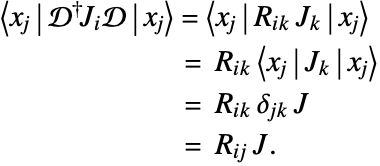Quantum-Mechanical Rotations

Rotations of quantum-mechanical objects (state ket or state bra vectors, operators, density matrices, and polarization moment expansions) are accomplished via the rotation operator, the matrix elements of which are given by the Wigner -functions. In the AtomicDensityMatrix package, these are provided by the WignerD function. (Note that as of Mathematica version 8.0, there is also a built-in WignerD function. The built-in version has slightly different syntax, given on its documentation page. To use either the built-in function or the ADM version, just use the appropriate syntax. The built-in function uses a different convention than the one described here, in which the Euler angles have the opposite sign.)

WignerD[{j,m1,m2},{alpha,beta,gamma}]	Wigner -function for angular-momentum quantum numbers j, m1, and m2 and Euler angles alpha, beta, and gamma
WignerD[j, {alpha, beta, gamma}]	matrix for rotation of an atomic system with angular momentum j
WignerD[s1,{alpha,beta,gamma},s2]	rotation matrix element between atomic states s1 and s2
WignerD[sys,{alpha,beta,gamma}]	matrix for rotation of atomic system sys

Rotation matrix elements.

In order to perform rotations, the Wigner rotation matrices must be applied to different types of objects in different ways, described in the tutorial below. Alternatively, the WignerRotate function can be used, which rotates an arbitrary quantum-mechanical object.

WignerRotate[x,{alpha, beta, gamma}]

rotate operator or irreducible tensor x using Wigner -functions

Rotating any quantum-mechanical object.

The way in which WignerRotate operates is determined by the form of the object to be rotated, as well as by two additional options. The RotationSense option specifies whether an active or passive rotation is desired, i.e., whether the state ("Active") or coordinate system ("Passive") should be rotated. A passive rotation is the inverse of the active rotation by the same angles; in this tutorial we consider active rotations, which are the default. The option StandardOperator distinguishes between the density matrix and all other operators, which have the same form but different rotational properties, as described below. The default value StandardOperator->False is appropriate for rotations of density matrices, polarization-moment decompositions of density matrices, and irreducible tensors that rotate in the normal way, including ket and bra vectors.

Options for WignerRotate.

Rotation of state bras and kets

Kets

A state ket can be expanded in the Zeeman basis as , where are the expansion coefficients, and we assume summation over repeated indices. The superscript index indicates that the form a contravariant set of tensor components. In the AtomicDensityMatrix package, state kets are represented by a column vector of their coefficients.

Here is a state ket—a spin-up state. It is written as a column vector, indicating that it is contravariant.

A rotation of into a rotated ket is accomplished by the rotation operator :

where the , called the Wigner -functions, are the matrix elements of in the Zeeman basis. Thus the expansion coefficients transform as . This is the prototype for the rotation of contravariant tensors.

The rotation operator for a rotation by an angle about an axis is given by , where is the angular-momentum operator. Rather than the axis-angle parameterization, however, arbitrary rotations are commonly expressed in terms of the Euler angles , , , as a rotation by about the -axis, followed by a rotation by about the -axis, followed by a rotation by about the -axis: .

WignerD gives the matrix elements of . Here is the rotation matrix for a system for a rotation by an angle about the -axis.

Here is the rotation applied to the state, producing a state with spin along the -axis. Operators operate on contravariant states (or irreducible tensors) from the left.

Here are the expectation values of the components of the angular-momentum operator for the spin- state.

And for the spin- state.

To produce a spin- state, we perform a rotation by about the -axis, using the Euler angles , , .

The expectation vector now points in the direction.

Bras

A state bra is expanded as , where are the covariant expansion coefficients. In the AtomicDensityMatrix package, state bras are represented by the row vector of their coefficients.

Taking the Hermitian conjugate of the expression , we find how a bra transforms under rotation: . Thus the expansion coefficients of a state bra transform as . This is the prototype for the rotation of covariant tensors.

In the matrix notation used in the package, covariant quantities must be acted on from the right. Thus we use the form of the transformation in which the -matrix is on the right:

We could also use the form in which the -matrix is on the left by writing an explicit sum over the components:

Rotation of operators

Standard operators

Rotations can be thought of as applying to operators rather than states. Performing a rotation on the expectation value of an operator , we have . Thus the operator transforms as .

The expectation value of the rotated operator with respect to the spin- state is the same as expectation value of the unrotated operator with respect to the spin- state.

The density matrix

Although the density matrix is an operator, its rotation transformation is the inverse of that for other operators. We can see this by noting that the expectation value of an operator with respect to a density matrix is given by . Then the expectation value under a rotation is given by , so ρ transforms as .

Rotate the density matrix about the -axis.

The spin now points along .

WignerRotate can also be used to rotate operators. However, since the density matrix transforms differently than other operators, the desired transformation must be specified with the option StandardOperator. This should be set to True if an operator other than the density matrix is being rotated, and False if the density matrix (or a state ket or bra) is being rotated. Because we will most commonly be manipulating the density matrix, the default value is StandardOperator->False.

Rotation of irreducible tensor operators

An irreducible tensor operator of rank is a set of operators (covariant) or (contravariant), , that transform under rotations like the Zeeman components of a bra or ket. Thus we have and .

Because irreducible tensor operators also rotate like standard operators, as above, we have and .

One example of an irreducible tensor operator is a vector operator written in the spherical basis.

The components also make up a rank-one irreducible tensor, which can be rotated according to the rule for covariant components, using the rotation matrix for a system. The same result is obtained.

For the components of the angular-momentum operator in the Cartesian basis, the relationship given above becomes , where is the rotation matrix for classical Cartesian vectors. We can use this to derive the classical rotation matrix. If , , are spinors pointing along the three Cartesian axes, first note that

where is the angular-momentum quantum number. For example, with :

Then we have

The Wigner -matrix for rotation of a spinor by an arbitrary set of Euler angles.

Find the same matrix using the built-in RotationMatrix function for rotations around , , and .

Rotation of polarization moments

The polarization operators , with , make up a complete set of basis operators for a system with angular momentum . Any operator can be expanded in terms of the polarization operators. For example, the density matrix is expanded as , where are the polarization moments.

The polarization moments form an irreducible tensor, and transform as a contravariant set. To see this, we consider a rotation of the density matrix, and then expand over the polarization operators: , so that the polarization moments transform as .

The polarization moments of each rank transform according to the rotation matrix for angular momentum . Here we perform a rotation about the -axis.

The spin points along .

As we saw above, the transformation under rotation for the density matrix is the inverse of that for other operators. For an expansion of an operator other than the density matrix, we have . Thus the expansion coefficients of a standard operator transform as .

Rotating larger systems

Rotation matrices for systems consisting of more than one level can be constructed by giving the level specification as an argument to WignerD or WignerRotate.

Here is the specification for a system consisting of a state and a state.