Observables
Observables[sys, ω, a]
returns the differential change in optical parameters of probe light with frequency ω and amplitude a upon propagation through a medium described by atomic system sys in terms of the rotating‐frame density‐matrix elements, assuming default light polarization and rotating‐wave transform.
Observables[sys,ω, a, pol]
returns the change in optical parameters for probe light of polarization specified by parameters pol.
Observables[sys, ω, (a, φ}, pol]
returns the change in optical parameters for probe light with phase φ.
Observables[sys, ω, a, pol, TransformMatrixu]
returns the change in optical parameters in terms of rotating‐frame density‐matrix elements assuming the rotating‐wave transform described by the matrix u.
Details and Options
- Observables returns the thin-medium differential change in probe field amplitude, phase, and polarization per unit path length in the medium and unit atomic density.
- For the default polarization parameterization "AngleEllipticity", Observables returns
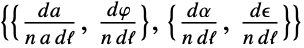, where d ℓ is the infinitesimal optical path length, a is the electric-field amplitude, φ is the optical phase, α is the polarization angle, ϵ is the ellipticity, and n is the atomic density. - The expressions returned by Observables are valid under the slowly varying envelope approximation, i.e., the assumption that the fractional change in the optical parameters is small over the distance of an optical wavelength.
- The atomic system sys is specified as a list of AtomicState objects.
- The following options for Observables are the same as those for OpticalField. A value of Automatic means that the default value specified for OpticalField will be used:
-
PolarizationVector Automatic reference polarization vector PropagationVector Automatic unit wave vector Parameterization Automatic parameterization scheme for polarization TimeVariable Automatic symbol used to represent time variable - The following options for Observables are the same as those for DensityMatrix. A value of Automatic means that the default value specified for DensityMatrix will be used:
-
TimeDependence Automatic whether density matrix elements should have explicit time dependence Representation Automatic Zeeman or polarization moment representation DMSymbol Automatic symbol to use for density matrix elements DMLabel Automatic additional label for density matrix elements ComplexExpandVariables Automatic whether to express density matrix elements in terms of real and imaginary parts - Observables takes the following additional options:
-
ExpandDipoleRME 
True whether to write the reduced dipole matrix element in terms of of the natural line width and other parameters TransformMatrix Automatic the unitary matrix used to transform from the laboratory frame to the rotating frame
Examples
open allclose allBasic Examples (2)
Expressions proportional to the fractional change in electric field amplitude, change of phase, change in polarization angle, and change in ellipticity of a field of frequency ω and amplitude a, in terms of the rotating-frame density-matrix elements. The field is assumed to have the default polarization (linear, along x) and propagation direction (along z), and a standard method is used to generate the rotating-wave transform.
We can simplify the expressions somewhat by assuming that the light frequency ω is approximately equal to the transition frequency Energy[2], by writing the electric-field amplitude a in terms of the Rabi frequency ΩR=ad, and by writing the transition frequency in terms of the transition wavelength λ=2π/Energy[2]:
In the above form, we can see that the expressions have the units of length squared (the units of the frequencies Γ and ΩR cancel, and the density-matrix elements are dimensionless). Thus by multiplying by a path length and the atomic density we obtain the changes in the dimensionless optical parameters.
In order to obtain correct results from a given calculation, it is vital that the light polarization and rotating-wave transformation used by Observables matches those used to produce the Hamiltonian used to generate the density-matrix evolution equations.
Define an elliptically polarized optical field with reference polarization vector along z, propagating along x.
The Hamiltonian for the atomic system subject to this optical field.
The change in light parameters for light of this polarization.